386
Level 2
Board Level
(presuming the same radius and the same volumetric flow),the resis-
tance increases.Mathematically this relationship is proportional,or:
(As the length increases, the resistance increases.)
Scenario 2: (Varying the Radius)
Assume there are two pipelines through which the same volumetric
flow of 10 liters/min is required. Which of these two pipelines, as
illustrated in
Figure 5,
would require more energy, hence offering
greater resistance?
Fig. 5
Effect of radius (area) on resistance
Clearly pipeline B will require more energy per volumetric flow
(higher resistance) than pipeline A. Therefore, as the radius de-
creases, the resistance increases. Mathematically this relationship
represents inverse proportionality, or:
(As the radius decreases, the resistance increases.)
Scenario 3:
(Varying Both the Length and the Radius)
Assume there are two pipelines through which the same volumetric
flow of 10 liters/min is required. Which of these two pipelines, as
illustrated in
Figure 6
, would require more energy, hence offering
greater resistance?
Fig. 6
Dominance of radius over length to resistance
Notice that in this case pipeline A is half the length of pipeline B
and also has a radius half that of pipeline B. We have already seen
from scenario 1 that a decrease in length results in a decrease in
resistance. In this scenario however,even though pipeline B is longer
by a factor of 2, pipeline A will require more energy per volumetric
flow than pipeline B. In other words, this scenario demonstrates
that changes in the radius affect the resistance faster than changes
in the length affect resistance. As a result, the power of the radius
in the inverse relationship is higher than the power of the length in
the proportional relationship.
The mathematics to demonstrate that power is really a fourth power
requires much more effort than is warranted for our purposes,
especially since the mathematics will not improve our intuitive
understanding of the equation. Therefore we will simply state that
resistance is related to the radius to the fourth power or
(Small changes in the radii produce absolutely enormous
changes in the resistance.)
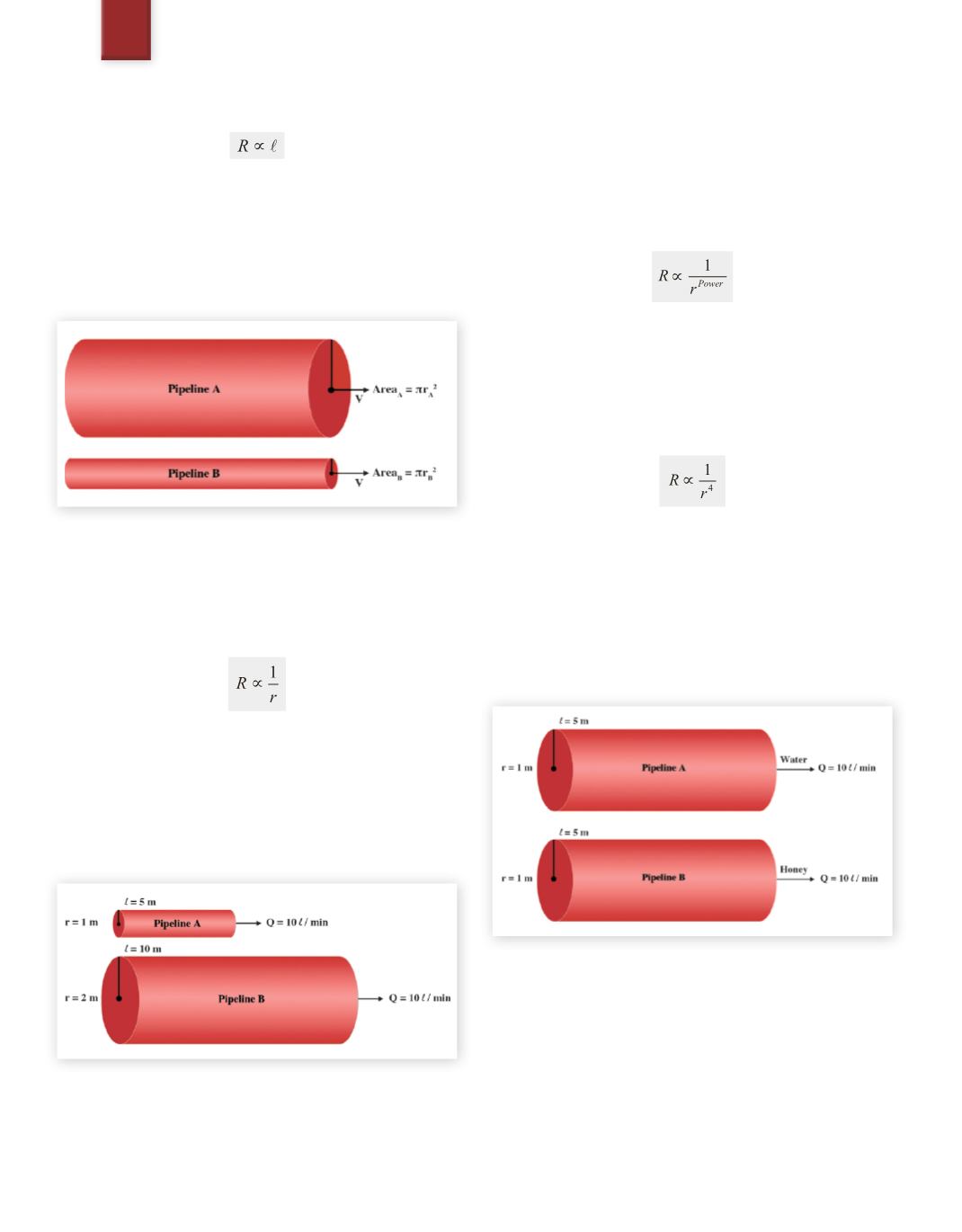
Scenario 4: (Varying Viscosity)
Let us again presume that there are two pipelines as depicted in
Figure 7
. Note that the pipelines are identical in both length and
radius and that they have identical volumetric flows. However,
pipelineA is transporting water and pipeline B is transporting honey.
Fig. 7
Effect of viscosity on resistance
Even though the dimensions of the flow conduits are the same,
pipeline Bwill requiremore energy to transport the same volumetric
flow. Clearly there is another parameter related to the fluid itself,and
not the flow path, which affects resistance. This other parameter is
the viscosity, usually designated by the Greek letter η. As defined in
Section 2.2, the viscosity is a measure of the‘sticky’ attraction of the
molecules within a fluid. By this definition honey would therefore
be more viscous than water.
SAMPLE PAGE


