Appendix A: Mathematics
521
A
variables increased and decreased together. When the relationship
was inversely related, the variables changed in inverse directions.
We now must discuss more complex relationships where the pow-
ers of the related variables are not always equal and not always
equal to 1. As mentioned in Level 1, understanding and interpret-
ing these more complex relationships will be the most important
mathematical tool you will develop both for taking the exam and
for truly understanding how ultrasound behaves in predicting the
body’s response to disease. As you progress through this book, you
will learn that many of the equations which dictate the behavior of
ultrasound and the behavior of the body with respect to disease will
behave in these complex non-linear fashions.
14.1 Direct Non-Linear Proportionality
As discussed in Section 10.1, the word direct implies that both re-
lated variables change in the same direction, or an increase in one
variable produces an increase in the related variable, and a decrease
in one variable produces a decrease in the related variable. Quite
frequently, the word direct is dropped and just assumed, so that the
word direct is implied in the expression non-linear proportionality.
In these complex cases where the powers of the two related variables
are not equal,a change in one variable will produce amore significant
change in the related variable. Unlike the simple case discussed in
Section 10.2, a change in one variable by a factor of
x
produces a
bigger change in the related variable than a factor of
x
. The following
example demonstrates a non-linear proportionality.
◊
Example :
y
= 3 ·
x
2
⇒
y
is proportional to
x
2
(Recall that the symbol (
⇒
) means “implies”)
If
x
= 1
⇒
y
= 3 · (1)
2
= 3
x
= 2
⇒
y
= 3 · (2)
2
= 12
x
= 5
⇒
y
= 3 · (5)
2
= 75
So an increase in x, results in a greater increase in y.
Similarly, a decrease in x results in a greater decrease in y,
or
y
α
x
2.
Note that for this example, a change in
x
by a factor of 2 results in a
change in
y
by a factor of 2
2
, or 4, clearly a non-linear relationship.
Fig. 4
y = 3x
2
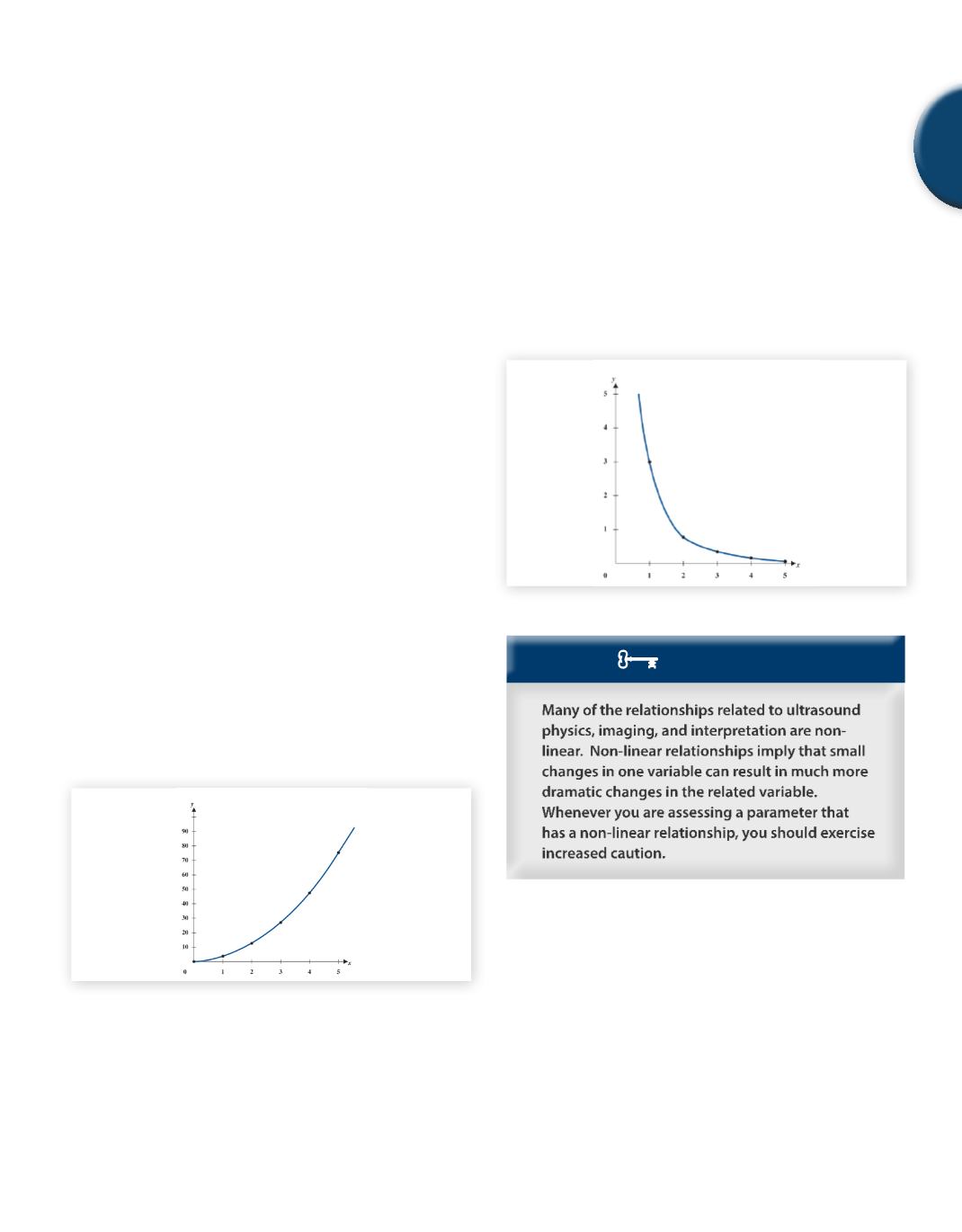
14.2 Complex - Inverse Proportionality
Asmentioned in Section 10.3,all inverse relationships are non-linear.
However,when the powers of the two variables are not equal and are
not equal to one,then amuchmore complex non-linear relationship
results. In the simple case when the powers are equal and equal to 1,
an increase in one variable by a factor of
x
produces a corresponding
decrease in the related variable by the same factor of
x
(and vice
versa). For more complex inverse relationships, a change in one
variable by a factor of
x
will produce a corresponding change in
the opposite direction not by the same factor of
x
, but by a power of
that factor
x
. In other words, small changes in one variable produce
significantly greater changes in the related variable.
◊
Example :
y
= 3/
x
2
⇒
y
is inversely proportional to
x
2
.
If
x
= 1
⇒
y
= 3/1
2
= 3
x
= 2
⇒
y
= 3/2
2
= 3/4
x
= 5
⇒
y
= 3/5
2
= 3/25
So if x increases a small amount, y decreases a much larger amount
or
y
∝
1/
x
2
Fig. 5
y
= 3/
x
2
KEY CONCEPT
15. Interpreting Relationships Within Linear
and Non-Linear Equations
Remember that these mathematical concepts are powerful tools
when understood well enough to be applied. In this section, we
will develop the skills necessary to apply these concepts to general
equations. We will start off with simple equations and work our
way toward seemingly more complex equations. However,since the
concepts to be applied are always the same, once you have adequate
exposure and experience in these concepts, even more complex
appearing equations will not present any greater challenge than
apparently simple equations.
SAMPLE PAGE


